Laundered Shop Towels: 12 - Everything gives you cancer...except laundered shop towels.

First, a little bit of background on looking at exposure to carcinogens:

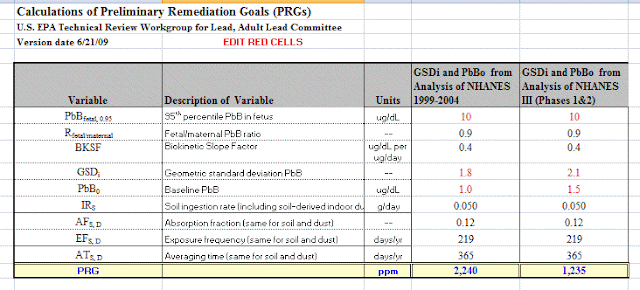
ATSDR recognizes that, at present, no single generally applicable procedure for exposure assessment exists, and, therefore, exposures to carcinogens are best assessed on a case-by-case basis with an emphasis on prevention of exposure. (1)

What this means is that we can provide no real method for dose/response when it comes to exposure to chemicals suspected to be carcinogens.  Therefore "0" exposure is recommended.

ATSDR recognizes that estimation of lifetime cancer risks is further complicated when available data are derived from less than lifetime exposures and that pharmacokinetic insights from animal models may be of utility in addressing this issue. (1)

What this means is that we can look at animal models to help us, but we lack data on a lifetime exposure to chemicals (70 years) so our estimates of a cancer risk will be lacking.

The lowest dose levels associated with carcinogenic effects are identified as cancer effect levels (CELs), with the stipulation that such a designation should not be construed to imply the existence of a threshold for carcinogenesis. (1)

Lowest dose found does not draw a line in the sand where below that is "no cancer" and above it is "cancer."

Also, exposures associated with upper- bound excess risk estimates over a lifetime of exposure (i.e., one case of cancer in 10,000 to one case of cancer in 10,000,000) as developed by EPA are presented. (1)

We look at dose in terms of a cancer risk.  CalEPA looks at a risk of cancer as one in 100,000 (10-5):

Source

CalEPA has developed a "No Significant Risk Level" (NSRL) of 15 ug/day for lead.  What this value is used for is to set a "safe harbor" amount for which the business does not have to post a Proposition 65 warning sign.  It assumes that a person could consume up to 15 ug of lead per day (2.14E-03 mg/kg-day) with out a risk of more than 1 additional cancer per 100,000.  15ug of lead dos not assume a "safe" threshold, it is used to establish an amount of lead whereby a Proposition 65 notification is not required.

When Gradient states that lead exceeded the CalEPA NSRL by "11" times:

(Gradient 2011 Report)

What exactly does a ratio of "11" mean in terms of risk?  Here is what ATSDR says about assessing exposure to a carcinogen:

Both exposure and toxicity information are necessary to fully characterize the potential hazard of an agent. ATSDR considers exposure to an agent to be "an event consisting of contact at a boundary between a human and the environment at a specific environmental contaminant concentration for a specified interval of time; the units to express exposure are concentration multiplied by time."  (1)

Gradient assumes that each time a laundered shop towel is handled by a worker - exposure - there will be intake of the metals that remained on the towel after it has been washed.  That intake is also referred to as a "dose" which ATSDR defines as:

"[t]he amount of contaminant that is absorbed or deposited in the body of an exposed individual over a specified time. Therefore, dose is different from, and occurs as a result of, an exposure."  (1)

In order for Gradient's model to be true, contaminants on the laundered shop towel must be deposited onto the hand and the hand must contact the mouth.  The "dose" will be the amount of contaminant on the hand that is transferred into the mouth.

Cancer risk is looked at differently from chemicals that do not contribute to cancer or cause health effects other than cancer.  Gere is what CalEPA says about exposure to carcinogens:

For chemicals that are listed as causing cancer, the "no significant risk level” is defined as the level of exposure that would result in not more than one excess case of cancer in 100,000 individuals exposed to the chemical over a 70-year lifetime. In other words, a person exposed to the chemical at the “no significant risk level” for 70 years would not have more than a “one in 100,000” chance of developing cancer as a result of that exposure. (2)

How does CalEPA calculate that "no significant risk level” for lead?

Source  Page 15

The "theoretical cancer potency" - qhuman - is also called the cancer slope factor.

Source

For lead, CalEPA uses the value 0.047 mg/kg-day-1 (see graphic at the top of this post).  Plugging in this value into the formula:

NSRL = (0.00001 x 70) / 0.47 = 0.0148 mg or 0.0148 * 1000 = 14.8 ug ~ 15 ug (ppb).

In other words, a person exposed to 15 ug (ppb) of lead for 70 years would not have more than a “one in 100,000” chance of developing cancer as a result of that exposure.

If we agree that 15 ug consumed for 17 years would  show more than one additional cancer per 100,000, what would Gradient's intake of 2.4E-03 mg/kg-day (0.168 mg)?

(Gradient 2011 Report)

In other words, if 15ug lead = 1 in 100,000, what would 0.168 mg lead result in?

Guess I'll need to calculate that.  Dang, more math...and I suck at math.  (Note to past self should time travel become a reality: Take math instead of computer programming in Fortran.)

Next post: Laundered Shop Towels: 13 - 100,000 workers using 12 towels per day


.

Laundered Shop Towels: 11 - Lead, a fetus, and a PPM.

What does the EPA have to say about lead when it develops clean up goals for lead contaminated soil?

In the commercial/industrial setting, the most sensitive receptor is the fetus of a worker who develops a body burden as a result of non-residential exposure to lead. Based on the available scientific data, a fetus is more sensitive to the adverse effects of lead than an adult.

We assume that cleanup goals (preliminary remediation goals or PRGs) that are protective of a fetus will also afford protection for male or female adult workers.

The model equations were developed to calculate cleanup goals such that there would be no more than a five per cent probability that fetuses exposed to lead would exceed a blood lead (PbB) of 10 micrograms lead per deciliter of blood (µg/dL). This same approach also appears to be protective for lead’s effect on blood pressure in adult males.

How much lead in soil consumed is necessary to produce 10 micrograms lead per deciliter of blood?

This is a fair and relevant question, and it relates to the problem with workers using laundered shop towels.

If Gradient is stating an "exceedance ratio" of "591" times the CalEPA MADL, which is the "maximum allowable dose levels for chemicals listed as causing birth defects or other reproductive harm" And the MADL for lead is based on "fetal development," then looking at how much lead consumed is required to produce "10 micrograms lead per deciliter of blood" - an actual quantitative amount of lead in the blood where we expect there will be adverse effects to the fetus above that level - would tell us how much total lead would need to be ingested to bring about that amount of lead in the blood.

Let's look at the variables EPA uses and the values they assigned:

EPA

Based on this, the consumption of 50 milligrams (0.050 grams) of soil containing up to 2,240 ppm of lead should be "protective of a fetus will also afford protection for male or female adult workers."

If 10,000 ppm is 1%, 2,240 ppm is 0.2%.  So...0.2% of the soil consumed puts into the blood the amount of lead to achieve 10 micrograms lead per deciliter of blood.

How much total lead would be consumed if 50 milligrams of soil containing 2,240 ppm of lead is ingested?

0.2% * 50 mg = 0.002 * 50 = 0.1 mg of lead

Based on a PRG of 2,240 ppm, EPA states:

A key concept is that a PRG is the average concentration of a chemical in an exposure area that will yield the specified target risk in an individual who is exposed at random within the exposure area.  Thus, if an exposure area has an average concentration above the PRG, some level of remediation is needed. (1)

The consumption of lead, and I am assuming from any source, of less than 0.1 mg per day, would not contribute to more than 10 ug/dl of lead in the blood, which is the amount of lead in the blood protective of a fetus.

What is the amount of lead per kg of body weight?

0.1 mg-day / 70 kg =  0.0014 = 1.4E-03 mg/kg - day

Since lead is the one metal that produced the highest "Exceedance Ratios of Individual Toxicity Reference Values for Exposure via Hand Contact - Typical Use (12 Towels)," what is applicable to lead will also be applicable for all the other lower "exceedance ratios" Gradient reports. (2)

So..

The MADL value of 0.5 ug-day lead is for "safe harbor" reporting to the public.  The EPA's PRG of 2,240 ppm (0.1 mg - day) is the clean up level for soil to yield a specified target risk of less than 10 ug/dl of lead in the blood deemed to be protective of the fetus.  Both the MADL and PRG are based on protecting a fetus but are calculated based on different assumptions.  The CalEPA's MADL assumes 1000 time less the NOAEL is "safe" for a fetus, and the EPA's PRG assumes a blood lead level of less than 10 ug/dL is "safe" for a fetus.

Which one appears to be a bit more sound?

How does the Gradient lead intake compare to the EPA PRG for lead?

0.0043 mg/kg-day (Gradient's intake value for lead)

0.0014 mg/kg-day (based on EPA's PRG of 2,240 ppm lead in soil)

That's an "exceedance ratio" of 3 times the safe lead level consumed which would be protective of a fetus.

Remember, that's based on Gradient's mean lead concentration they reported (post), the transfer of 13% of the lead from the towel to the hand (post), the transfer of 13% of the lead on the hand to the mouth (post), 12 exposures per day, 245 days a year, performed for 40 years.

How does it look if an HTE of 6% is used? (post)

0.0019 mg/kg-day  (Gradient's intake value for lead using 6% for the HTE)

That's an "exceedance ratio" of 1.3 times the safe lead level consumed which would be protective of a fetus.

How does it look if the CalEPA hand to mouth calculation is used? (post)

0.0022 mg/kg-day (CalEPA calculation for lead)

That's an "exceedance ratio" of 1.6 times the safe lead level consumed which would be protective of a fetus.

You may be tempted to tell me "See!  It's still above a safe threshold using any of those calculations!"  For which I will remind you that those intakes are based on a mean lead concentration on the towel of 100 mg/kg.  Go to the report and look at the range of lead concentrations Gradient lists (Table 4 page 7).

Those values also assume that there will be a transfer of lead from a towel that was washed in water with soap and heat dried, equivalent to 13% of the lead evenly distributed on the towel from which 75% of the surface area comes in contact with the hand.

Oh, and it also assumes that this will happen 12 times a day, and that each time the hand will contact the mouth and some value of lead will be consumed.

All of those things must happen in order to get an "exceedance ratio" that is higher than the "safe" threshold.

There is one more thing that needs to be considered as well.  The CalEPA equation calculates the intake per day.  The PRG value of 2,240 ppm is based on exposure to the soil for a year.

In other words, we would expect (assume) a person coming in contact with soil containing 2,240 ppm of lead for one year, to produce a blood level of no more than 10 ug/dL.  That ppm is based on an exposure frequency (EF) of 219 days and an averaging time (AT) of 365 days.

This EPA PRG model assumes that there will not be constant exposure to soil containing lead, but assume there will be 219 days of exposure and 0.05 grams of soil will be consumed each time there is exposure.  Based on this, 2,240 ppm of lead or less is deemed to be protective.

For an exposure period of one day, lead intake during one work day (12 towels in 8 hours) - using CalEPA's equation (see post) - can be calculated as follows:

• Intake = 0.0013 mg/cm2 x 19 cm2 x 0.5 x 1.5/hour x 8 hours =  0.148 mg per work day
• 0.148 mg per day = 0.148 / 70 kg =  0.0022 mg/kg-day Intake or 2.2E-03 mg/kg-day

Using Gradient's EF of 245 days and an AT of 365 days (instead of 40 years to be consistent with the EPA lead PRG calculation), we would modify the CalEPA calculation by multiplying the mg/kg intake by 245 and dividing that number by 365.

• (0.0022 mg/kg-day * 245 days) / 365 days = 0.0015 mg/kg-day or 1.5E-03 mg.kg-day

Over a 365 day period a 70 kg worker using 12 towels a work day with an average lead load of 100 mg/kg (ppm) would have an average intake of lead of 0.0015 mg/kg-day.

If this same worker was exposed to soil contaminated with lead, the intake of lead would need to be less than 0.0014 mg/kg-day.

Using CalEPAs calculation, Gradient's values, and a 365 day averaging time, the "exceedance ratio" will be 0.0015/0.0014 = 1.07, or 1.1, or 1 = even.  This average amount of lead reported by gradient will produce a blood lead level of less than 10 ug/dL even when 12 towels are used and the worker places the finger and palm to the mouth each time a towel is used.  This is protective of the worker because it is protective of the fetus!

So the question now is: If lead had the highest "exceedance ratio" reported by Gradient, and you are now presented with CalEPA apples and EPA apples to compare Gradient apples with, are you still concerned about laundered shop towels creating any risk of a reproductive health concern for a worker, even a pregnant one?

Well...

Cancer!!!  What about the risk of cancer?



Next post: Laundered Shop Towels: 12 - Everything gives you cancer...except laundered shop towels.


.

Laundered Shop Towels: 10 - When is an average not average?

Rule number 5: Always make sure the model and equations reflect reality.


I think I have presented enough justification to throw out Gradient's  "Intake of metals in laundered shop towels via hand contact" equation:

Instead, I believe the CalEPA equation to be a lot more sound and valid for calculating a hand to mouth intake, even though it uses assumptions I think are a bit of a stretch as well.  Still, we need something to quantitatively estimate an intake so we can look at risk, so this equation will have to do for workers using laundered shop towels.

Guideline for Hand-to-Mouth Transfer of Lead through Exposure to Consumer Products: 2011

The CalEPA equation calculates the daily total intake.  To compare apples with apples and oranges with oranges (Rule Number 4), The intake was divided by 70 kg (weight of an adult) to derive a mg/kg-day intake value (see last post).

I commented on how close the CalEPA method intake values match the values I calculated when the Hand to Mouth transfer efficiency (HTE) rate was changed to a more appropriate 6% for an adult.  But that comparison I made is like comparing apples with oranges.

The CalEPA intake is based on a single uptake event and is used as a threshold to meet the California Proposition 65 "Safe Harbor" designation.

A business has “safe harbor” from Proposition 65 warning requirements or discharge prohibitions if exposure to a chemical occurs at or below these levels. These safe harbor numbers consist of no significant risk levels (NSRL) for chemicals listed as causing cancer and maximum allowable dose levels (MADL) for chemicals listed as causing birth defects or other reproductive harm. (1)

As long as a business can keep the exposure below the NSRL or MADL (whichever is lowest) the business does nor have to post Proposition 65 warnings.  The assumption here is that below these levels there would be little risk for cancer or reproductive/birth defects.  What it does not imply is that above those values there is risk.  Risk is related to dose, the lower the dose, the lower the risk.  NSRLs and MADL attempt to draw a line in the sand - one side is "no risk" and the other side is some.

The problem with the Prop 65 notice is that it does not communicate a degree of risk, only that there is risk. One cancer in 99,998 or one cancer in 98 gets the same warning:

Gradient assumes that laundered shop towels that contain concentrations of metals above these thresholds represent risk to the worker, hence the black and red bar graphic I showed in the first post on this topic:

Source

A bit confusing for it shows copper as having a higher exceedance than lead.  Anyway, it is based on information from this table:

2011 Gradient Study

Ignore the maximum intakes they reported - they are statistically impossible to reproduce in a real world situation (see post).  Look instead at the average (mean) intake value for lead, which is the metal that presents the highest exceedance ratio compared to a threshold.

Using the intake equation Gradient developed for hand to mouth exposure, Gradient reports exceeding the CalEPA MADL and NSRL for lead for average laundered shop towel usage by a worker.

Using the CalEPA equation and the same average towel usage and average lead metal loading used by Gradient, I calculate the following exceedance "ratios" for lead:

• Intake (lead) = 0.0022 mg/kg-day
• MADL = 0.0000071 mg/kg-day (0.5 ug/day) (2)
• NSRL = 0.00021 mg/kkg-day (15 ug/day) (2)

This would generate an "exceedance ratio" of:

• MADL = 309 x
• NSRL =  10 x

Well, heck, that's lower but still pretty high.  At least that's what one could reasonably conclude when comparing apples with oranges.

Let's look at the "maximum allowable dose levels (MADL) for chemicals listed as causing birth defects or other reproductive harm."  Here is what the CalEPA based the lead "safe harbor" MADL on:

CalEPA 2008 Page 13

That "safe" value of  0.0000071 mg/kg-day is based on fetal development, which is only applicable to a female worker who is pregnant and using the laundered shop towels.  That "safe" threshold - MADL - is not applicable to a male worker's intake using the same laundered shop towels.

Let's look a bit closer on how that MADL for lead is calculated.

The MADL is the level at which chemicals listed for reproductive toxicity would have no observable effect assuming exposure at 1,000 times that level. (3)

What is the " no observable effect" level?

No-observed-adverse-effect level (NOAEL): The highest tested dose of a substance that has been reported to have no harmful (adverse) health effects on people or animals. (4)

No-Observed-Adverse-Effect Level (NOAEL)—The dose of a chemical at which there were no statistically or biologically significant increases in frequency or severity of adverse effects seen between the exposed population and its appropriate control.  Effects may be produced at this dose, but they are not considered to be adverse. (5: Page 526)

Neither ASTDR nor IRIS identify a NOAEL for lead,  instead they use a blood lead level as a "safe" dose.

So if we assume that the lead MADL is based on an effect to the fetus, and we assume that the lead MADL of 0.5 ug-day is 1000 times lower than the NOAEL, the NOAEL used by CalEPA must be 500 ug-day (0.5 x 1000 = 500).  I can find nothing on how CalEPA derived the value "0.5 ug-day" other than this and this.

A NOAEL of 500 ug-day is equal to 7.14 ug/kg-day or 0.007 mg/kg-day (based on 70 kg body weight).  0.007 = 7.0E-03

Gradient reported an average "typical use" intake for lead of 4.2E-03 (Table 8 Page 13).  Even using all of Gradient's assumptions and their intake formula, the intake they report is below the No-observed-adverse-effect level used by CalEPA (7.0E-03).  An average use of 12 towels per day for five days a week, for 245 days per year for 40 years falls below the lowest concentration reported to show no adverse effects.

Still not convinced that these laundered shop towels pose no increase of risk to a worker, even a pregnant one exposed to a mean concentration of lead at 100 ppm?  Well, let's look at it another way.

What is the amount of lead in soil that would be considered to present a risk for a person who ingests 50 mg of soil each day for a total of 219 days in a year?

In other words, under certain assumptions, what would the clean-up level for the lead in the soil be?

Next post: Laundered Shop Towels: 11 - Lead, a fetus, and a PPM.


.

Laundered Shop Towels 9 - CalEPA's Lead Intake from Direct Hand-to-Mouth Contact

The equation Gradient has developed to calculate worker intake of metals, such as lead, is based on a number of assumptions.

Not only do we have to accept the mean concentrations Gradient reports for these metal contaminants on the laundered shop towels, but we are also asked to assume that 13% of those contaminants will be transferred from the towel to the hand after the towel had been washed with soap and heat dried.

On top of this, as my last post described, Gradient makes the assumption that each time a laundered shop towel is used, the worker will place his hand to his mouth and 13% of the contaminants on the towel will be transferred to the mouth - intake.

Even if you accept Gradient's intake equation, it is difficult to accept the values they assigned for the assumptions used.

In my last post I detailed why the HTE of 13% Gradient uses is incorrect and an HTE is more appropriated since it involves calculating the HTE using both an adult soil consumption value and an adult hand.

Recalculating the intake values using an HTE of 6% still shows some metals to be above regulatory standards.  This is primarily due to the inappropriateness of calculating the HTE as a ratio of daily soil consumption to amount of soil found on both hands - as was discussed in my last post.

There is a more appropriate way to go about figuring out a hand to mouth transfer, which once again brings up:

Rule number 5: Always make sure the model and equations reflect reality.

Here is how CalEPA looks at lead intake from direct hand to mouth contact, which is the model Gradient should have used to calculate the intake of metals - such as lead - from laundered shop towels.

Source Page 6

Gradient instead calculates a lead intake over a worker's entire working lifetime of 40 years, whereas CalEPA calculates it on a single contact performed i number of times (events).  According to CalEPA:

There can be multiple hand-to-mouth contacts during the use of a given consumer product.  Thus the total direct lead intake via the use of a given consumer product will be the sum of intake from each contact i during product use.

CalEPA modifies the equation above as follows:

Source Page 6

Let's look at how CalEPA calculates the values for these parameters in their equation:

Source Page 11

                                     Surface area (SAD)

Source Page 12

                                    Contact frequency (λD) = Frequency
                         
                                    Exposure Duration (t) = Time


Lhand-D can then be calculated as follows:

Note: To keep consistent with other values used (see below), the surface of the front of the hand will be calculated as 840 (total surface area of both hands) * 0.5 (for one hand) * 0.5 (for the front of the hand).  Thus, the surface area for the front of one hand will be: 210 cm2.  In my previous "fun with graph paper" post, I estimated the surface area to be 188 cm2.

If Lhand-D is:

The lead loading on the part of the hand touching the mouth (not the loading of the whole hand), in units of weight per surface area (e.g., mass of lead per surface area of the fingertip, μg/cm2).

Assuming that 13% of the 75% lead load on the laundered shop towel is transferred to the hand:

• 0.00127 x 2268 x 0.75 x 0.13 = 0.28 mg
• 0.28 mg / 210 cm2 = 0.0013 mg/cm2 or 1.3 ug/cm2

 The "part of the hand touching the mouth" or SAD, is calculated as follows: 

Assumed for workers in occupational settings that the surface area of the hands contributing to the hand-to-mouth exposure pathway was 5% of the palmar surface of the hand, or 10 cm2.

Here is what I found in an earlier version of this CalEPA Lead document:

Source 2008

For this post, I will use the adult male SAD of 19 cm2.

Fdirect will be 50% (as per CalEPA)

Contact frequency (λD) will be 1.5 towels per hour (based on 12 laundered shop towels per 8 hour shift)

Exposure Duration (t) will be an 8 hour work shift.

For an exposure period of one day, lead intake during one work day (12 towels in 8 hours) - using CalEPA's equation - can be calculated as follows:

• Intake = 0.0013 mg/cm2 x 19 cm2 x 0.5 x 1.5/hour x 8 hours =  0.148 mg per work day
• 0.148 mg per day = 0.148 / 70 kg =  0.0022 mg/kg Intake or 2.2E-03

That's how CalEPA would calculate the intake based on a mean lead concentration of 100 mg and a towel to towel transfer efficiency of 13% - which are the same values Gradient uses in their equation.

Here is how the CalEPA method and equation stacks up against the Gradient equation and assumptions for the metals they reported with concentration exceedance ratios.

CalEPA Formula source

Notice how the CalEPA's equation produces an intake very similar to the values Gradient calculated for cancer intake.  Interesting.

Now lets look at the CalEPA method using an HTE of 6% (see post):

Notice how the CalEPA intake is very similar to the intake values obtained using Gradient's equation with an HTE of 6%.  Interesting.

The question you should now ask is: What equation more accurately estimates the intake if the assumptions used are valid?

I say we go with the CalEPA equation.  Now all we need to focus on will be the assumptions regarding the average load on the towel, the towel transfer efficiency, and the number of laundered shop towels used per day by a worker.  Oh yeah, we will also need to look at the respective "toxicity criteria" these intakes were compared to and how Gradient went about "evaluating the magnitude of the exceedances."

Next Post: Laundered Shop Towels: 10 - When is an average not average?


.

Laundered Shop Towels 8: A child's hand is not an adult's hand

That title is one of those "duh!" types of statements.

So if that's true, why did Gradient base the hand to mouth efficiency (HTE) on studies involving 1-6 year olds?

Not that there is anything wrong with that, but in this case, we are dealing with adult workers and assumptions should have been made using adult data - that was readily available to them.

Gradient states in their 2003 study the following:

Gradient used the median skin surface area data specific to a 1- to 6-year-old child and applied the soil AF derived from Roels to estimate the average mass of soil on the hands for a 1- to 6-year-old child, which is approximately 145 mg for both hands.

A median soil ingestion rate of 38 mg/day for children ages 1 to 6 years was calculated based on a soil ingestion study conducted in Amherst, Massachusetts.

This soil ingestion rate was divided by the hand soil-loading estimate for a child resident (approximately 145 mg on both hands), for a daily HTE value of approximately 0.26 hand loads per day.

In this report, we used half of 0.26 as the HTE value for adults, or 0.13. 

Using a smaller HTE for adults as compared to children is further supported by the United States Environmental Protection Agency's (USEPA) soil ingestion rates:  their recommended mean soil ingestion rate for adults is exactly one-half of the value for children less than 6 years of age (USEPA, 1997a)

That HTE value of 13% was based on dividing the amount of soil a child consumes in a day by the amount of soil both hands of a child can hold (soil-loading).  Read my previous post on this for more information.

That amount, 26%, was then divided in half to represent the HTE for an adult, 13%.

Sounds good until you think about it a little more closely.  See it?  Yeah, you can fly a Russian Antonov An-225 through this one.

According to Gradient, the "145 mg for both hands" was calculated as follows:

Gradient then divided the average amount of soil adhering to the hands by the “available” skin surface of the hands for the average age of the children included in the Roels study (i.e., 11-yearolds) to generate a soil adherence factor (AF) of 1.1 mg/cm2 for both boys and girls.  

The skin surface area of the hands available for contact with soil is assumed to be approximately one-third of the total surface area of both hands.

If that assumption holds true, why didn't Gradient use "one-third of the total surface area of both hands" for an adult?

To get the HTE of 13% the "median soil ingestion rate of 38 mg/day for children ages 1 to 6 years" was divided by "145 mg for both hands."

If we assume (according to the EPA) that the "mean soil ingestion rate for adults is exactly one-half of the value for children less than 6 years of age," wouldn't it have been more appropriate to take one-half of 38 mg/day - 19 mg/day - and divide that by  "one-third of the total surface area of both hands" for an adult?

If that assumptions for a child holds true, this would have been a more appropriate - or scientifically sound - method to calculate the HTE for an adult worker.

You can ask Gradient why they did not use this method to calculate their HTE.  Even more peculiar is why they did not use an established calculation to estimate hand to mouth intake for an adult.  A little bit of Google searching brings up this document from the CalEPA:

Guideline for Hand-to-Mouth Transfer of Lead through Exposure to Consumer Products

Here is what CalEPA says on page 12:

The U.S. EPA Exposure Handbook provides representative hand surface area values for both adults and children in Chapter 6, General Factors for Dermal Route.  Detailed data distributions of hand surface area (mean, standard deviation and percentile distributions) by gender and age are provided in Tables 6-2 to 6-8 (U.S. EPA, 1997). 

Gosh...I wonder what that source is?

U.S. Environmental Protection Agency (U.S. EPA, 1997). Exposure Factors Handbook.  National Center for Environmental Assessment, Office of Research and Development, Washington, DC, EPA/600/p-95/002F a-c.

That sounds familiar...I wonder where I saw that source mentioned before?  Oh, yeah, it was referenced in the 2003 Gradient study on laundered shop towels:

Source: 2003 Gradient Study

Why's that important?  Well in that EPA handbook is data that Gradient should have used.  Here is what CalEPA goes on to say:

From the U.S. EPA Exposure Handbook, the representative value of the surface area of both hands in adults is 750 cm2 for women and 840 cm2 for men. 

I wonder what the HTE would be if we used the values assigned to adults?  Let's see:

"The skin surface area of the hands available for contact with soil is assumed to be approximately one-third of the total surface area of both hands."  So if we multiply 840 by 0.33 we get 274 cm2

"Gradient then divided the average amount of soil adhering to the hands by the “available” skin surface of the hands...to generate a soil adherence factor (AF) of 1.1 mg/cm2 for both boys and girls."  So if we multiply 274 by 1.1 we get 301 mg on both hands, this is the "soil loading" estimate.

If the adult "mean soil ingestion rate for adults is exactly one-half of the value for children less than 6 years of age," we would take 38 mg/day and divided it by 2, which would give us 19 mg/day. 

 "This soil ingestion rate was divided by the hand soil-loading estimate...for a daily HTE value..." So, if we divide 19 by 301 we would get an adult male HTE of  6%.

As I pointed out in a previous post, this method of calculating an HTE is flawed because it assumes all the soil ingested in a day comes solely from the hands.

Still, though, if Gradient was going to calculate an HTE based on this method, it would have made more sense to use adult values, which would have been calculated as 6%.

Does an HTE of 6% instead of 13% affect their findings?

Recalculation - Table 8 of 2011 Study

I had to tweak the "Average Load" values in Table 8 upwards to get the same intake values they calculated.  The values in blue represent the intakes one would see if a 6% HTE was used.  At a 6% HTE, the Exceedance Ratios in Table 8A are changed as follows:

You can see that there are still exceedances, but adjusting just one variable, the HTE, changes the results considerably.  Now, consider the other parameters "assumed" to be correct by Gradient.  Every value that is used that is higher than would actually be in reality (mean. maximum, towel transfer efficiency, number of rags used), exaggerates the "exceedance ratios" Gradient reports.

Yeah...but look at lead!  It's still 273 times higher than CalEPA's MADL.... and five times higher for cancer.  Explain that!

Those exceedance values are only applicable if you accept Gradient's HTE..  Remember, Gradient calculated that percentage based on ALL of the soil consumed in a day coming from the hands.  13% or 6% is based on that premise, which is not the sole mechanism for soil intake into the child or adult. (see post).

A better way to calculate how much lead (metal) would be transferred from the hand to the mouth would have been to use a more plausible calculation....like the one that CalEPA has developed.

Next Post: Laundered Shop Towels 9: CalEPA's Lead Intake from Direct Hand-to-Mouth Contact


.

Laundered Shop Towels: 7 - Fun with graph paper.

I got to thinking about what is involved in Gradient's model and equation.  That is, if there is intake of lead each and every time a laundered shop towel is handled, how would this transfer from hand to mouth take place in a work environment.

According to the model:

Source

And the equation:

Source

The lead (metal) is transferred to the hand through a "towel to hand transfer efficiency" or "Tt/h" which I discussed in a previous post.  The Tt/h is a unitless number in Gradient's equation, and is a percent (0.13) of what is on calculated to be on the towel (Loadtowel) surface (mean/maximum).

What Gradient's equation states is this.  If the towel contains X amount of lead per square centimeter, the towel will dislodge 13% of X that is on each centimeter of towel.  They then go on to calculate that the hand will only come in contact with 75% (Ftowel)  of the towel's surface area (SAtowel).

On the hand will be 13% of X from 75% of the towel.

Gradient assumes that the towel has the lead (metal) evenly dispersed on each of the 2,268 square centimeters that make up a laundered shop towel's surface area.  The "load" is found on Table 2 of the report.  For lead, it is as follows:

• Average = 0.0012  mg/cm2
• Maximum = 0.0075  mg/cm2

If we are looking at the average concentration of lead found (mean) each square centimeter of the towel's surface is considered to contain 0.0012 mg/kg of lead.

The hand, coming in contact with 75% of the laundered shop towel's surface area, is assumed to dislodge 13% of the lead onto the hand. (let's ignore N for the time being)

• 0.0012 x 2268 x 0.75 x 0.13 = 0.26 mg

Gradient assumes that each towel with an average concentration of 100 mg/kg of lead will place onto the hand 0.26 mg of lead.

This is where it get's a bit...complicated.

Gradient assumes that the hand with the 0.26 mg of lead will come in contact with mouth, and when it does, 13% of that amount will end up in the mouth (intake).

They base that 13% hand to mouth transfer efficiency (HTE) on the how much soil is consumed in a day by a child divided by how much soil is contained on a 1-6 year old's hand.  They then cut that percentage in half because " The smaller HTE value used for adults reflects the reduced hand-to-mouth behavior in people greater than 6 years of age."  You can read more about this in my last post.

But back to where I was going with this.

If the HTE is 13% like Gradient assumes it is, how would 13% of 0.26 mg be transferred from the hand to the mouth?

Rule number 5: Always make sure the model and equations reflect reality.

Regardless of what studies one looks at, the model and calculation you develop must reflect the actual reality for the situation you are describing.

If we are to assume that an employee places his hands to his mouth each and every time they use a laundered shop towel, then we must assume there is a plausible mechanism for this to take place.

If the shop towel transfers and evenly spread out load of lead onto the hand, how much of the hand needs to come in contact with the mouth to transfer 13%?

Gradient assumes that the transfer efficiency is 13%.  That is, if the whole hand was placed into the mouth, only 13% of the lead would come off the hand.

Think about that for a minute.

Gradient is basing the intake on the efficiency of transfer.  That is, each square centimeter of hand surface area that came in contact with the towel can only transfer 13% of that load into the mouth.

This requires one of two things.

1. The whole contact surface area of the hand is placed into or up to the mouth
2. The 75% surface area of the laundered shop towel only comes in contact with the the part of the hand that comes in contact with the mouth.

Do any of those two situations seem plausible?

Because the assumption for the HTE is flawed, the amount of metals, such as lead, Gradient calculates getting into the body is flawed as well.

And this is why my question of "how" is important.

To have 13% lead transfer from the hand to the mouth, either the whole hand is placed into the mouth or licked, or 13% of the surface area of the hand is contacted with the mouth for 100% transfer efficiency (which is not what their equation is based on).

Let's assume that we have 100% transfer efficiency (which is not supported by any of the studies they looked at).  How much surface area of the hand would need to come in contact with the mouth?

Once again, we need to look at Gradient's model and equation.  Gradient assumes that only one hand is used in their equation, which means that the total amount of lead, 0.26 mg, will reside on one hand and it will be that hand that contacts the mouth.  It also appears that they assume only the front of the hand (palm and inside fingers/thumb) come in contact with the towel.

So here is what I did, when I got to thinking about this.

How much surface area of an employees hand would come in contact with the laundered shop towel?

This required a one centimeter by one centimeter sheet of graph paper, and a pen.

I roughly calculated the surface area of my hand by taking the total surface area of the box (345 square centimeters) and subtracting the number of boxes outside of the outline (157).  Based on my calculations (and you can see why I am not an engineer), the surface area of my hand that could come in contact with a laundered shop towel is 188 square centimeters.

I'm stepping out on a limb here, but assuming I have a two dimensional flat surface hand, how much of that surface area represents 13%?

For the finger tips, it looks like this:

Red blocks = 13% of total hand surface area

For the palm, it looks like this:

Red blocks = 13% of total hand surface area

It is reasonable, I think, to assume that if the hand contacts the mouth it would do so either at the fingertips or the palm.  The question then comes down to this:

1. Is it reasonable to assume that much of the fingertips or palm will contact the mouth each and every time an employee picks up a laundered shop towel?
2. Is it reasonable to assume that 100% of the metal in that area will be removed from the hand and put into the mouth?

In the two graphics above, each red square assumes a transfer efficiency (HTE) of 100%.  In gradients equation, the hand to mouth transfer efficiency (HTE) is 13%.  In order to get to get 13% of 0.26 mg of the lead now on the hand into the mouth, how much surface area of the hand needs to contact the mouth?

Gradient assumes that 75% of each square centimeter of the laundered shop towel transferred onto the hand 13% of the load.

If the "average" load for lead is 0.0012 mg/cm2, then  0.26 mg total of lead must be transferred onto the front of the hand.  If we assume a 13% HTE (as Gradient does) how much surface area of the hand would need to contact the mouth to give an intake of  0.34 mg of lead (0.26 x 0.13)?

In order for Gradient's equation to work, the metal must be evenly distributed all over the face of the hand.  If you assume that it is on the fingertips only, then the assumption is the fingertips are the only part of the hand that contacts the mouth.  Same goes for the palm.

But that's not what their equation assumes.  It assumes a transfer efficiency of 13% each and ever time the laundered shop towel is used.

How is this done?  Gradient assumes that the entire surface area of the hand contacts the mouth.

In order to get 0.34 mg of lead into the body, a hand with the surface area of 188 square centimeters must have 0.014 mg of lead on each square centimeter (0.26/188), assuming a HTE of 13%.

To limit the part of the hand to the mouth, condenses the amount of contaminant per square centimeter and also assume that only that part of the hand will contact the mouth.

For a hand with a surface area of 188 square centimeters that will contact 75% of the laundered shop towel, Gradient's calculation assumes that this much of the hand will have contact with the mouth.

That's right, each and every one centimeter square box inside the outline of my hand will need to contact the mouth each and every time a laundered shop towel is used.

Do the math:

• 0.0012 x 2268 x 0.75 x 0.13 x 0.13  = 0.034 mg of lead into the mouth.

Question: How much of the hand must come in contact with the mouth if there is a 13% HTE that takes place each and every time a laundered shop towel is used?

Answer: The whole surface of the hand.

Does that look anything like their graphic is showing?

Does their equation represent reality for a worker using a laundered shop towel?

Still not convinced that their report is flawed and that laundered shop towels do not pose an increase in risk even remotely close to their calculations??

Read on.

Next post: Laundered Shop Towels 8: A child's hand is not an adult's hand.

.

Laundered Shop Towels: 6 - Finger Lickin' Good!

The basis for Gradient's model is that each laundered shop towel will transfer 13% of the load from 75% of the towels surface area onto the hand.  The hand will then be placed to the mouth and 13% of what is on the hand will be transferred into the mouth.  That second "13%" transfer is what Gradient calls a hand to mouth efficiency - "HTE" - value:

The HTE transfer is based on estimates of the amount of soil transferred by children from the surface of their hands to the mouth, where it is subsequently ingested, but is adapted for adults, based on a lower HTE value, to be consistent with the lower ingestion rate of adults. (Page 9)

Here is how Gradient came up with this value (excerpt from their 2003 study)

Daily Hand to Mouth Transfer Efficiency. To estimate the amount of metal on the hands that might be ingested via hand-to-mouth contact, we used a hand transfer efficiency, or HTE parameter, of 0.13. 

The HTE parameter quantifies the fraction of material on the hands that is likely to be transferred to the mouth and ultimately ingested. 

The HTE transfer is based on estimates of the amount of soil transferred by children from the surface of their hands to the mouth, where it is subsequently ingested.

Gradient used the median skin surface area data specific to a 1- to 6-year-old child and applied the soil AF derived from Roels et al. (1980) to estimate the average mass of soil on the hands for a 1- to 6-year-old child, which is approximately 145 mg for both hands. 

Gradient then combined the estimate of soil loading on the hand with an estimated soil ingestion rate to derive the hand transfer efficiency (HTE) value, which is an estimate of the fraction of the mass of soil adhering to the hands that would need to be ingested to yield the estimated daily soil ingestion rate. 

Read that last paragraph again.  I'll wait.  And while you are reading it, here is some music to set the mood.  With that premise, Gradient came to this:

A median soil ingestion rate of 38 mg/day for children ages 1 to 6 years was calculated based on a soil ingestion study conducted in Amherst, Massachusetts. 

This soil ingestion rate was divided by the hand soil-loading estimate for a child resident (for a child resident (approximately 145 mg on both hands), for a daily HTE value of approximately 0.26 hand loads per day.

If you are reading this and paying close attention you will see what they have done and why it should be viewed as inappropriate for this study.  If you want to read about the Amherst, Massachusetts, you can see a summary about it here.  Let's look at the first part of the abstract for the Calabrese & Stanek paper:

Sixty-four children aged 1-4 years were evaluated for the extent to which they ingest soil. [t]he present study included a number of modifications from the Binder et al. study. The principal new features were (1) increasing the tracer elements from three to eight; (2) using a mass-balance approach so that the contribution of food and medicine ingestion would be considered; 

See it? 

"contribution of food and medicine ingestion would be considered"

The "median soil ingestion rate of 38 mg/day" is based on the amount of soil consumed from ALL sources, not just from the hands.  Gradient has based the HTE on 38 mg/day of soil intake coming from the hands only.

For this to be true, the soil on the hands, 145 mg, would need to be placed on the hands - no more - no less - and no other soil consumed in the day.  To obtain an HTE of 0.26 all the soil intake had to come from the hands - both of them.

Gradient assumes that the child licks, touches, contacts the mouth with both hands so that 0.26 of the soil on both hands is transferred to the mouth.  The 38 mg/day is from all sources, including dust, mouth soil on surfaces, food, and contact with other sources throughout the day.

Gradient goes on to say:

In this report, we used half of 0.26 as the HTE value for adults, or 0.13. The smaller HTE value used for adults reflects the reduced hand-to-mouth behavior in people greater than 6 years of age. 

Using a smaller HTE for adults as compared to children is further supported by the USEPA soil ingestion rates: their recommended mean soil ingestion rate for adults is exactly one-half of the value for children less than 6 years of age.

I assume that the HTE is the same for one hand (their model) as for both hands.  Basically, as I understand it, Gradient assumes that 13% of what is on the hand will be transferred to the mouth.

You can see where they came up with that 13%.  It assumes that because 38 mg/day of soil is consumed for a child, and an adult consumes half that amount, it all had to come from the hand.

That's not true of course, soil consumption comes from many sources in a day, not just from the hands.  But I'll go with it for now...I'll assume that there is a transfer rate of 13% of the load on the hand into the mouth.

And once again I am perplexed to understand how that would happen.  What's the mechanics involved?

Kimberly-Clark tells us that "an average person touches their face 16 times per hour."  Does that mean a worker places one hand to his mouth each time he picks up a laundered shop towel?

And when the worker places his hand to his mouth, does he lick his fingers or rub his lips over the surface of the hand that contacted the towel?  And if this happens each and every time 12 towels are used per day, how much area of the hand would need to contact the mouth so that 13% of the load that is evenly distributed on the hand is transferred to the mouth?

For Gradient's model and equation to hold true, the hand must contact the mouth and 13% of what is on the hand must transfer to the mouth.  How?

Next post: Laundered Shop Towels: 7 - Fun with Graph Paper


.