Should we accept it based on the reputation of Gradient and the credentials of the three authors? Or should we look deeper into the study to see how they came up with data that affords Kimberly-Clark the ability to ask workers: Why risk it? Who's counting on you?I then went on to say:
Well I have looked into it. I can support my conclusion that there is no additional risk to a worker using a laundered shop towel. Period. Should you believe me? No, not until you read what I am putting forth as my reasons why this study is flawed and their conclusion false.
So here we are after 13 posts on this topic. I have presented how Gradient came to conclude that there is a risk
Kimberly-Clark sure wants to take Gradient's findings at face value. What business wouldn't want to show how bad the other option is by claiming:
"Two studies conducted during the last 8 years show that laundered shop towels contain toxic heavy metals even after laundering." (1)
And they get to do that with unabashed glee simply because of a study prepared interdependently by:
Let's look at each one of my issues with their model, calculation, and assumptions. If there is an increase in risk high enough to warrant discontinuing the use of laundered shop towels, it must be supported by the science presented in Gradient's reports.
Gradient claims that the average concentration of lead (the metal with the highest exceedance ratios -Table 8a) in laundered shop towels is 100 mg/kg. If that average is not correct, then none of the intake values they calculated are correct.
Based on the minimum and maximum concentrations they present in Table 4 of their study, and the standard deviation reported, it is evident that the average Loads they use are skewed to represent a higher concentration of metals than would naturally be found.
The calculated mean - or average - is supposed to represent the true mean of the population. Based on the high variability in the concentrations they report (as shown by the standard deviation exceeding the mean) it is highly unlikely that the averages they used to determine the Load represent what is actually found on a laundered shop towel. It is, in most likelihood, magnitudes higher than what would normally be found.
Let's look at an example to illustrate this:
Here are 25 values representing the lowest concentration detected (1.7) and the highest (600) for lead. All the other numbers are just numbers I came up with. The numbers in blue represent all the values less than the mean, the numbers in red represent concentrations higher than the mean. Using these numbers I was able to get close to the mean and standard deviation reported by Gradient.
Since 100 mg/kg is the number Gradient uses to estimate the lead Load on the laundered shop towel, if these were the actual values detected, 22 towels encountered would have a concentration of lead on them less than 100 and three would be above.
In a normal distribution, "100" would be the average encountered. so at the end of the day, after handling 12 shop towels, the load encountered would be around 100. That's based on a normal distribution, where 100 is in the middle, half lower and half higher. In my example 92% of the towels encountered have a lead concentration lower than 100. See previous post on this topic.
I don't know what the actual concentrations for lead are, but I do know that the average of 100 is not a true representation of what is normally found on laundered shop towels. It is too high based on the standard deviation reported. This means that the Load for the towel they calculated is too high as well.
Even if the mean concentrations Gradient reports were correct, there is still the issue on whether or not the metals can be dislodged from the towel and onto the hand. That's the whole purpose of calculating a Load, to see what is available to enter the mouth from the hand. I discussed that issue in this post, and it is extremely relevant in determining the validity of their intake values.
The fact that an object may contain a high concentration of metals does not warrant concern if those metals can not be transported into the receptor, in this case from the hand into the worker's mouth. In order for Gradient's model to hold true, metals must come off the towel and onto the hand - Tt/h. Why Gradient did not look at what, if any, metals could dislodge from the towels is beyond me. Even Adam and Jamie of the Mythbusters could have figured out a sound way to determine this. And they're not PhDs!
So I'll call the "Load" and "Tt/h" part of Gradient's calculation:
But let's look at Load from a different angle. Gradient claims that the intake of lead a worker might encounter on laundered shop towels is "11" times higher than the CalEPA NSRL for lead. That is, the lead Load is significant enough to bring about 10 additional cancers for every 100,000 workers using laundered shop towels. (We would expect one cancer at the NSRL). See previous post.
As I showed in that post, 100,000 workers would use 11.8 billion laundered shop towels. Are you willing to contend that the 25 shop towels Gradient tested represent the Load on 11.8 billion towels?
Not only are the Load values Gradient used in question, but the intake they calculated requires the worker to place their hand to their mouth each time a laundered shop towel is used. For these exceedance values to be true, a worker must bring their hand (single) to their mouth 117,600 times (12 towels, 245 day, 40 years). And each time they bring their hand to their mouth, 13% of what is on the hand comes off the hand and is consumed.
Where did Gradient come up with that number of 13%? That number is half the amount of soil a child consumes if all of the soil consumed came from the hands. Read my post on this for more information on how Gradient derived this.
Why Gradient chose to use a child's hand and not an adults when calculating this transfer efficiency can only be answered by them. Had they used an adult's hand, the HTE would have been 6%. But that's still based on a faulty premise that all of the soil consumed by the adult came solely from the hands.
A better - or more sound - method would have been to use CalEPA's hand to mouth calculation (see post). Once again, why Gradient made up their own method for deriving an HTE can only be answered by them. It does seem odd though, that they would use CalEPA's MADL and NSRL thresholds and not their methodology. Peculiar.
Based on this, I'll call the "HTE" part of Gradient's calculation "Busted" as well:
And what about Kimberly-Clark's claim:
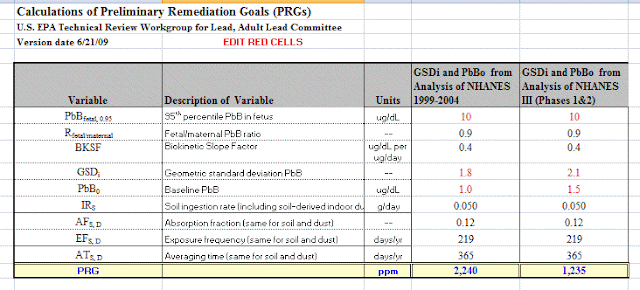
What Gradient should have done was calculate potential exposure risk using EPA's method for determining the clean up level of lead in soil, which is also based on the health of he fetus (post). EPA's "preliminary remediation goals (PRG) are based on the amount of lead intake from soil that would bring about a level of lead in the blood harmful to the fetus. At that blood level concentration of lead, Gradient's intake value exceeds the EPA 'safe" level by 3 times. Using the more appropriate 6% HTE (based on an adult hand), the exceedance ratio is 1.3 - using all the other assumptions and values used by Gradient. 3600 times higher refers to a value used to determine when signage and notification is not required by a business.
So I'll call Kimberly-Clark's claim in their brochure:
There you have it. I've shown you theirs...and I've shown you mine.
Should you believe Kimberly-Clark when they state:
You have read my posts and can easily check my sources and work my calculations. Here is what I think, based on what my research into this matter has shown me:
Which leads me to only one conclusion - Gradient's study and conclusion is....
Next post: Laundered Shop Towels: 15 - Why I spend the effort
.
"an environmental and risk science consulting firm renowned for their expertise in Toxicology, epidemiology, Risk Assessment, Product Safety, Contaminant Fate and Transport, and Environmental/Forensic Chemistry." (1)But those ratios Gradient reports in Table 8a have a much different meaning when you look at how they were generated as well as what the comparison is made to:
Let's look at each one of my issues with their model, calculation, and assumptions. If there is an increase in risk high enough to warrant discontinuing the use of laundered shop towels, it must be supported by the science presented in Gradient's reports.
Gradient claims that the average concentration of lead (the metal with the highest exceedance ratios -Table 8a) in laundered shop towels is 100 mg/kg. If that average is not correct, then none of the intake values they calculated are correct.
Based on the minimum and maximum concentrations they present in Table 4 of their study, and the standard deviation reported, it is evident that the average Loads they use are skewed to represent a higher concentration of metals than would naturally be found.
The calculated mean - or average - is supposed to represent the true mean of the population. Based on the high variability in the concentrations they report (as shown by the standard deviation exceeding the mean) it is highly unlikely that the averages they used to determine the Load represent what is actually found on a laundered shop towel. It is, in most likelihood, magnitudes higher than what would normally be found.
Let's look at an example to illustrate this:
Here are 25 values representing the lowest concentration detected (1.7) and the highest (600) for lead. All the other numbers are just numbers I came up with. The numbers in blue represent all the values less than the mean, the numbers in red represent concentrations higher than the mean. Using these numbers I was able to get close to the mean and standard deviation reported by Gradient.
Since 100 mg/kg is the number Gradient uses to estimate the lead Load on the laundered shop towel, if these were the actual values detected, 22 towels encountered would have a concentration of lead on them less than 100 and three would be above.
In a normal distribution, "100" would be the average encountered. so at the end of the day, after handling 12 shop towels, the load encountered would be around 100. That's based on a normal distribution, where 100 is in the middle, half lower and half higher. In my example 92% of the towels encountered have a lead concentration lower than 100. See previous post on this topic.
I don't know what the actual concentrations for lead are, but I do know that the average of 100 is not a true representation of what is normally found on laundered shop towels. It is too high based on the standard deviation reported. This means that the Load for the towel they calculated is too high as well.
Even if the mean concentrations Gradient reports were correct, there is still the issue on whether or not the metals can be dislodged from the towel and onto the hand. That's the whole purpose of calculating a Load, to see what is available to enter the mouth from the hand. I discussed that issue in this post, and it is extremely relevant in determining the validity of their intake values.
The fact that an object may contain a high concentration of metals does not warrant concern if those metals can not be transported into the receptor, in this case from the hand into the worker's mouth. In order for Gradient's model to hold true, metals must come off the towel and onto the hand - Tt/h. Why Gradient did not look at what, if any, metals could dislodge from the towels is beyond me. Even Adam and Jamie of the Mythbusters could have figured out a sound way to determine this. And they're not PhDs!
So I'll call the "Load" and "Tt/h" part of Gradient's calculation:
But let's look at Load from a different angle. Gradient claims that the intake of lead a worker might encounter on laundered shop towels is "11" times higher than the CalEPA NSRL for lead. That is, the lead Load is significant enough to bring about 10 additional cancers for every 100,000 workers using laundered shop towels. (We would expect one cancer at the NSRL). See previous post.
As I showed in that post, 100,000 workers would use 11.8 billion laundered shop towels. Are you willing to contend that the 25 shop towels Gradient tested represent the Load on 11.8 billion towels?
Not only are the Load values Gradient used in question, but the intake they calculated requires the worker to place their hand to their mouth each time a laundered shop towel is used. For these exceedance values to be true, a worker must bring their hand (single) to their mouth 117,600 times (12 towels, 245 day, 40 years). And each time they bring their hand to their mouth, 13% of what is on the hand comes off the hand and is consumed.
Where did Gradient come up with that number of 13%? That number is half the amount of soil a child consumes if all of the soil consumed came from the hands. Read my post on this for more information on how Gradient derived this.
Why Gradient chose to use a child's hand and not an adults when calculating this transfer efficiency can only be answered by them. Had they used an adult's hand, the HTE would have been 6%. But that's still based on a faulty premise that all of the soil consumed by the adult came solely from the hands.
A better - or more sound - method would have been to use CalEPA's hand to mouth calculation (see post). Once again, why Gradient made up their own method for deriving an HTE can only be answered by them. It does seem odd though, that they would use CalEPA's MADL and NSRL thresholds and not their methodology. Peculiar.
Based on this, I'll call the "HTE" part of Gradient's calculation "Busted" as well:
And what about Kimberly-Clark's claim:
"Just how far did they exceed these limits? Here’s one example: the study found that a worker using a typical number of shop towels per day can be exposed to up to 3,600 times the health-based exposure limit set for lead." (4th page)What does that mean, "3600 times?" That health based exposure limit is the CalEPA MADL for lead, and had Kimberly-Clark been more forthcoming, they would have let the worker know that the value CalEPA uses is based on health of the fetus and is set 1000 times lower than the no observable health effects level described in the literature. See this post and this post.
What Gradient should have done was calculate potential exposure risk using EPA's method for determining the clean up level of lead in soil, which is also based on the health of he fetus (post). EPA's "preliminary remediation goals (PRG) are based on the amount of lead intake from soil that would bring about a level of lead in the blood harmful to the fetus. At that blood level concentration of lead, Gradient's intake value exceeds the EPA 'safe" level by 3 times. Using the more appropriate 6% HTE (based on an adult hand), the exceedance ratio is 1.3 - using all the other assumptions and values used by Gradient. 3600 times higher refers to a value used to determine when signage and notification is not required by a business.
So I'll call Kimberly-Clark's claim in their brochure:
There you have it. I've shown you theirs...and I've shown you mine.
Should you believe Kimberly-Clark when they state:
Heavy metals have been found in laundered shop towels in amounts that exceed health-based exposure guidelines related to cancer and non-cancer related health issues, like reproductive and developmental effects.Should we still conclude that laundered shop towels pose a risk to workers?
You have read my posts and can easily check my sources and work my calculations. Here is what I think, based on what my research into this matter has shown me:
Which leads me to only one conclusion - Gradient's study and conclusion is....
Next post: Laundered Shop Towels: 15 - Why I spend the effort
.