Laundered Shop Towels: 7 - Fun with graph paper.

I got to thinking about what is involved in Gradient's model and equation.  That is, if there is intake of lead each and every time a laundered shop towel is handled, how would this transfer from hand to mouth take place in a work environment.

According to the model:

Source

And the equation:

Source

The lead (metal) is transferred to the hand through a "towel to hand transfer efficiency" or "Tt/h" which I discussed in a previous post.  The Tt/h is a unitless number in Gradient's equation, and is a percent (0.13) of what is on calculated to be on the towel (Loadtowel) surface (mean/maximum).

What Gradient's equation states is this.  If the towel contains X amount of lead per square centimeter, the towel will dislodge 13% of X that is on each centimeter of towel.  They then go on to calculate that the hand will only come in contact with 75% (Ftowel)  of the towel's surface area (SAtowel).

On the hand will be 13% of X from 75% of the towel.

Gradient assumes that the towel has the lead (metal) evenly dispersed on each of the 2,268 square centimeters that make up a laundered shop towel's surface area.  The "load" is found on Table 2 of the report.  For lead, it is as follows:

• Average = 0.0012  mg/cm2
• Maximum = 0.0075  mg/cm2

If we are looking at the average concentration of lead found (mean) each square centimeter of the towel's surface is considered to contain 0.0012 mg/kg of lead.

The hand, coming in contact with 75% of the laundered shop towel's surface area, is assumed to dislodge 13% of the lead onto the hand. (let's ignore N for the time being)

• 0.0012 x 2268 x 0.75 x 0.13 = 0.26 mg

Gradient assumes that each towel with an average concentration of 100 mg/kg of lead will place onto the hand 0.26 mg of lead.

This is where it get's a bit...complicated.

Gradient assumes that the hand with the 0.26 mg of lead will come in contact with mouth, and when it does, 13% of that amount will end up in the mouth (intake).

They base that 13% hand to mouth transfer efficiency (HTE) on the how much soil is consumed in a day by a child divided by how much soil is contained on a 1-6 year old's hand.  They then cut that percentage in half because " The smaller HTE value used for adults reflects the reduced hand-to-mouth behavior in people greater than 6 years of age."  You can read more about this in my last post.

But back to where I was going with this.

If the HTE is 13% like Gradient assumes it is, how would 13% of 0.26 mg be transferred from the hand to the mouth?

Rule number 5: Always make sure the model and equations reflect reality.

Regardless of what studies one looks at, the model and calculation you develop must reflect the actual reality for the situation you are describing.

If we are to assume that an employee places his hands to his mouth each and every time they use a laundered shop towel, then we must assume there is a plausible mechanism for this to take place.

If the shop towel transfers and evenly spread out load of lead onto the hand, how much of the hand needs to come in contact with the mouth to transfer 13%?

Gradient assumes that the transfer efficiency is 13%.  That is, if the whole hand was placed into the mouth, only 13% of the lead would come off the hand.

Think about that for a minute.

Gradient is basing the intake on the efficiency of transfer.  That is, each square centimeter of hand surface area that came in contact with the towel can only transfer 13% of that load into the mouth.

This requires one of two things.

1. The whole contact surface area of the hand is placed into or up to the mouth
2. The 75% surface area of the laundered shop towel only comes in contact with the the part of the hand that comes in contact with the mouth.

Do any of those two situations seem plausible?

Because the assumption for the HTE is flawed, the amount of metals, such as lead, Gradient calculates getting into the body is flawed as well.

And this is why my question of "how" is important.

To have 13% lead transfer from the hand to the mouth, either the whole hand is placed into the mouth or licked, or 13% of the surface area of the hand is contacted with the mouth for 100% transfer efficiency (which is not what their equation is based on).

Let's assume that we have 100% transfer efficiency (which is not supported by any of the studies they looked at).  How much surface area of the hand would need to come in contact with the mouth?

Once again, we need to look at Gradient's model and equation.  Gradient assumes that only one hand is used in their equation, which means that the total amount of lead, 0.26 mg, will reside on one hand and it will be that hand that contacts the mouth.  It also appears that they assume only the front of the hand (palm and inside fingers/thumb) come in contact with the towel.

So here is what I did, when I got to thinking about this.

How much surface area of an employees hand would come in contact with the laundered shop towel?

This required a one centimeter by one centimeter sheet of graph paper, and a pen.

I roughly calculated the surface area of my hand by taking the total surface area of the box (345 square centimeters) and subtracting the number of boxes outside of the outline (157).  Based on my calculations (and you can see why I am not an engineer), the surface area of my hand that could come in contact with a laundered shop towel is 188 square centimeters.

I'm stepping out on a limb here, but assuming I have a two dimensional flat surface hand, how much of that surface area represents 13%?

For the finger tips, it looks like this:

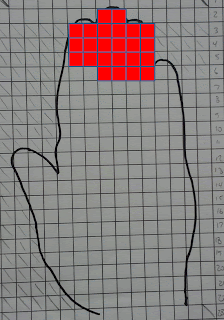Red blocks = 13% of total hand surface area

For the palm, it looks like this:

Red blocks = 13% of total hand surface area

It is reasonable, I think, to assume that if the hand contacts the mouth it would do so either at the fingertips or the palm.  The question then comes down to this:

1. Is it reasonable to assume that much of the fingertips or palm will contact the mouth each and every time an employee picks up a laundered shop towel?
2. Is it reasonable to assume that 100% of the metal in that area will be removed from the hand and put into the mouth?

In the two graphics above, each red square assumes a transfer efficiency (HTE) of 100%.  In gradients equation, the hand to mouth transfer efficiency (HTE) is 13%.  In order to get to get 13% of 0.26 mg of the lead now on the hand into the mouth, how much surface area of the hand needs to contact the mouth?

Gradient assumes that 75% of each square centimeter of the laundered shop towel transferred onto the hand 13% of the load.

If the "average" load for lead is 0.0012 mg/cm2, then  0.26 mg total of lead must be transferred onto the front of the hand.  If we assume a 13% HTE (as Gradient does) how much surface area of the hand would need to contact the mouth to give an intake of  0.34 mg of lead (0.26 x 0.13)?

In order for Gradient's equation to work, the metal must be evenly distributed all over the face of the hand.  If you assume that it is on the fingertips only, then the assumption is the fingertips are the only part of the hand that contacts the mouth.  Same goes for the palm.

But that's not what their equation assumes.  It assumes a transfer efficiency of 13% each and ever time the laundered shop towel is used.

How is this done?  Gradient assumes that the entire surface area of the hand contacts the mouth.

In order to get 0.34 mg of lead into the body, a hand with the surface area of 188 square centimeters must have 0.014 mg of lead on each square centimeter (0.26/188), assuming a HTE of 13%.

To limit the part of the hand to the mouth, condenses the amount of contaminant per square centimeter and also assume that only that part of the hand will contact the mouth.

For a hand with a surface area of 188 square centimeters that will contact 75% of the laundered shop towel, Gradient's calculation assumes that this much of the hand will have contact with the mouth.

That's right, each and every one centimeter square box inside the outline of my hand will need to contact the mouth each and every time a laundered shop towel is used.

Do the math:

• 0.0012 x 2268 x 0.75 x 0.13 x 0.13  = 0.034 mg of lead into the mouth.

Question: How much of the hand must come in contact with the mouth if there is a 13% HTE that takes place each and every time a laundered shop towel is used?

Answer: The whole surface of the hand.

Does that look anything like their graphic is showing?

Does their equation represent reality for a worker using a laundered shop towel?

Still not convinced that their report is flawed and that laundered shop towels do not pose an increase in risk even remotely close to their calculations??

Read on.

Next post: Laundered Shop Towels 8: A child's hand is not an adult's hand.

.